Занятие «Раскраски графов» факультативного курса «Элементы теории графов и ее приложения»
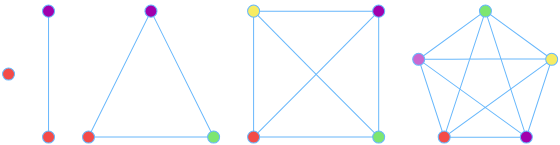
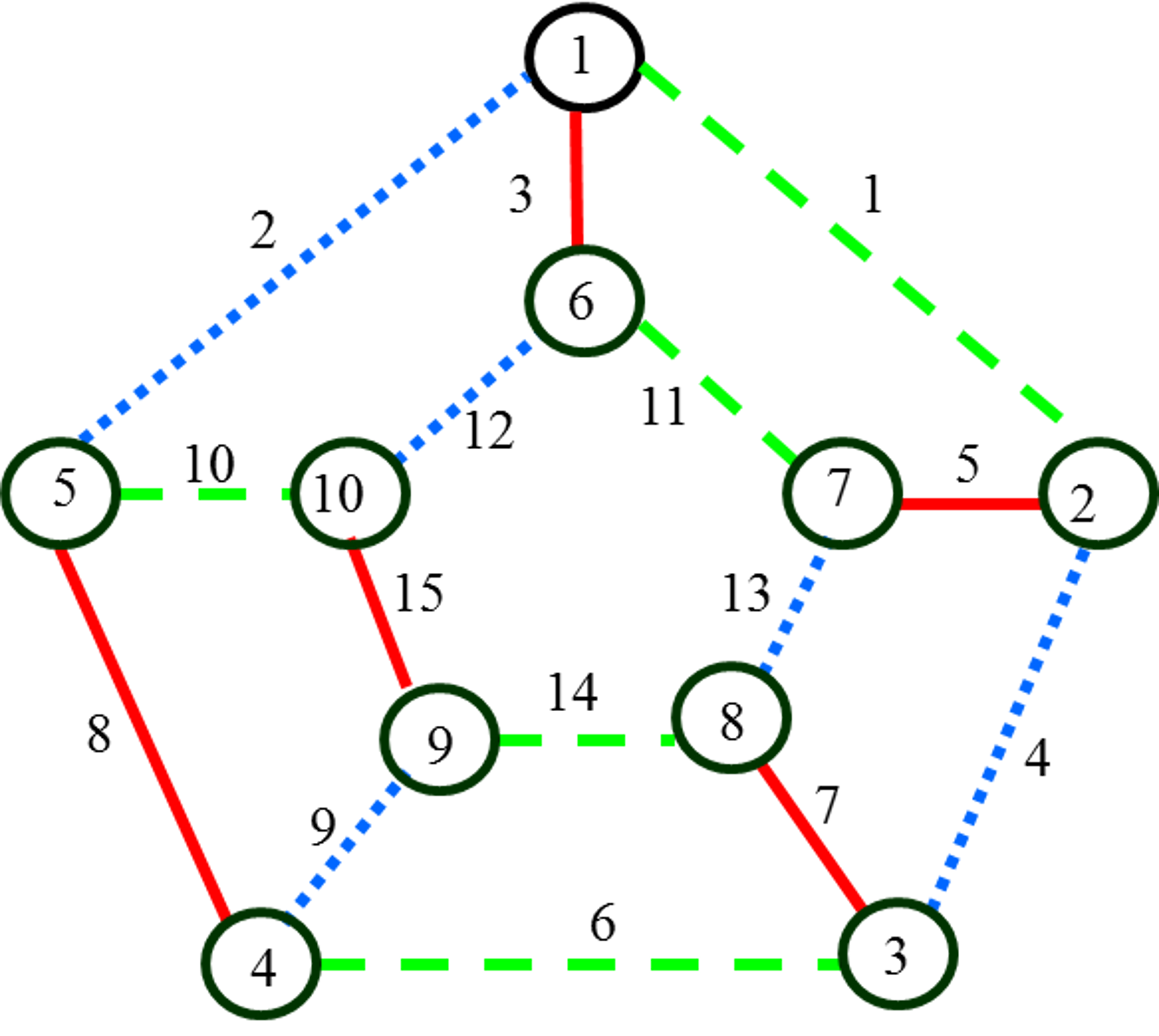
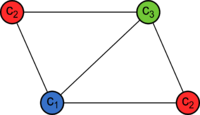
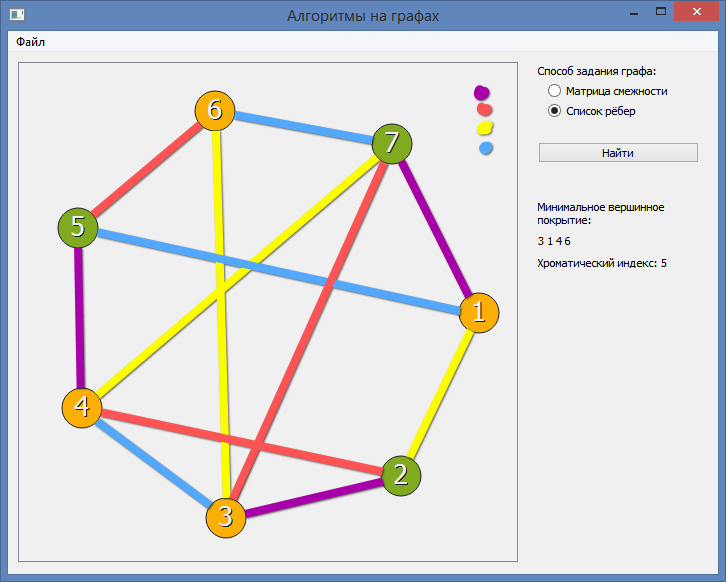
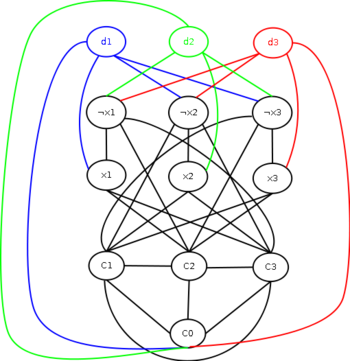
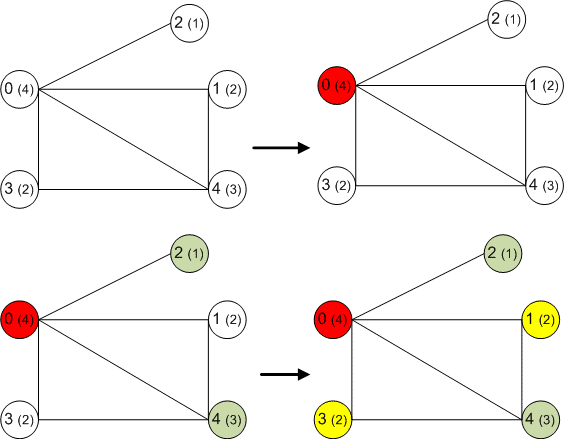
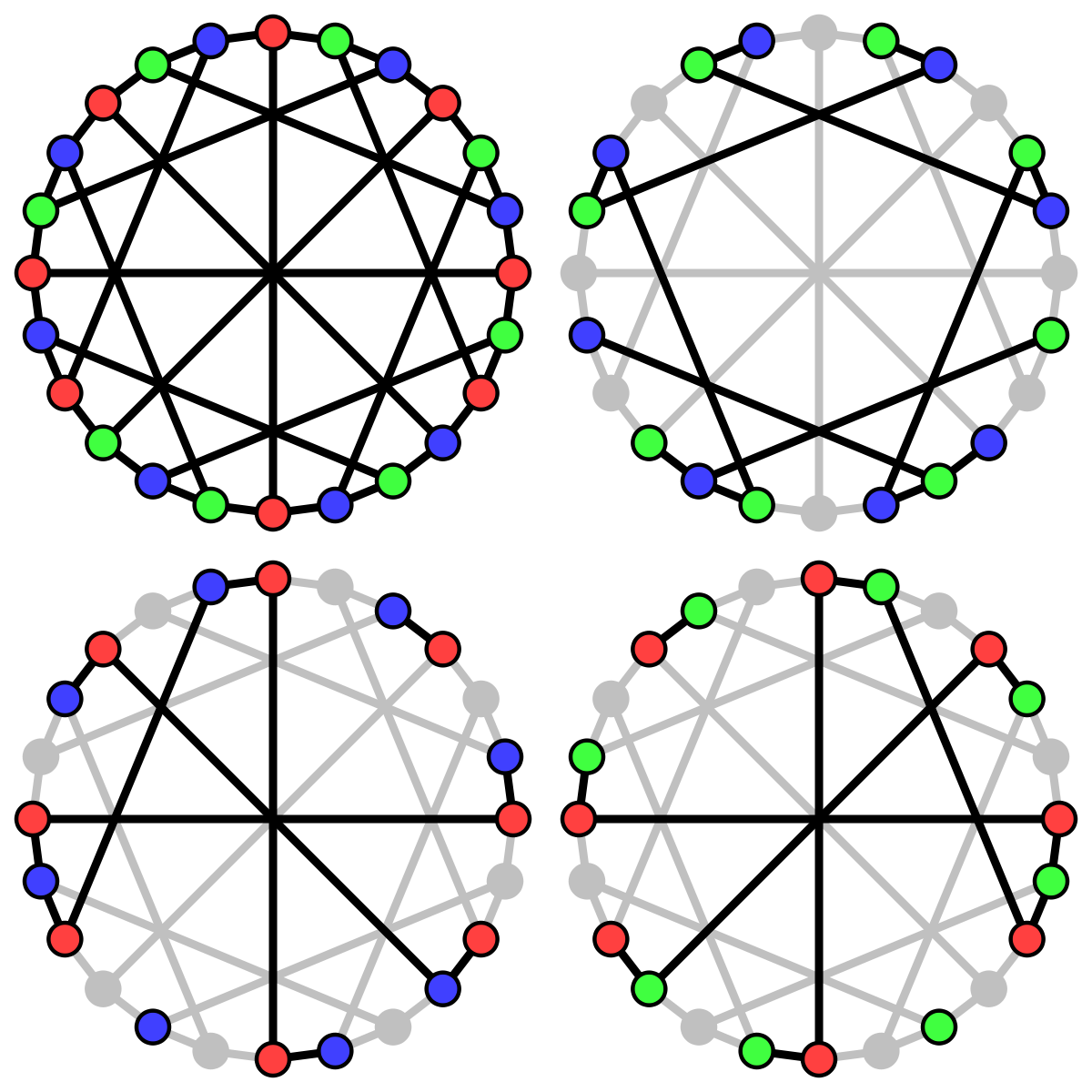
Раскраска графа — теоретико-графовая конструкция, частный случай разметки графа. При раскраске элементам графа ставятся в соответствие метки с учётом определённых ограничений; эти метки традиционно называются «цветами». В простейшем случае такой способ окраски вершин графа , при котором любым двум смежным вершинам соответствуют разные цвета, называется раскраской вершин. Аналогично раскраска рёбер присваивает цвет каждому ребру так, чтобы любые два смежных ребра имели разные цвета [ 1 ]. Наконец, раскраска областей планарного графа назначает цвет каждой области, так, что каждые две области, имеющие общую границу, не могут иметь одинаковый цвет. Раскраска вершин — главная задача раскраски графов, все остальные задачи в этой области могут быть сведены к ней.

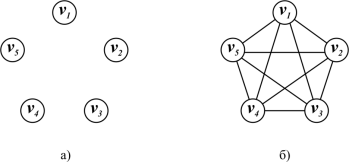





Работа выполнена в Учреждении Российской академии наук Институте математики им. Соболева Сибирского отделения РАН. Защита состоится 9 сентября г. Соболева Сибирского отделения РАН по адресу: г. Новосибирск, пр.




Статья посвящена анализу проблемы раскраски графа , актуальной в различных областях, включая составление учебных расписаний , планирование и управление ресурсами и многих других. В ходе исследования эта задача была адаптирована для оптимизации расписания учебных занятий. Основной целью исследования стало создание алгоритма и программного обеспечения для разработки пользовательского интерфейса расписания в учебных учреждениях. Разработанный софт может быть легко настроен для различных типов учебных заведений: от школ до университетов.